Rzeczy niemożliwe robię od ręki… Czyli Hipoteza Riemanna

Zawsze uważałem, że nie ma rzeczy niemożliwych. Grupa matematyków zakładała, że jest kilka problemów matematycznych, których nie da się rozwiązać. Jak uważałem, że na daną chwilę, nie ma na to narzędzi i pomysłu.

Właśnie jeden z tych problemów został rozwiązany, a autorem pracy jest słynny, brytyjski matematyk Sir Michael Atiyah. Naukowiec ten do tej pory zdobył już dwie bardzo ważne nagrody: Medal Fieldsa i Nagrodę Abela. Są one tak ważne, jak Narody Nobla.

Informatyka, czy ludzie chcą tego, czy nie, opiera się na matematyce.

Wszystkie algorytmy to przecież czysta matematyka. Jest to przecież królowa nauk. Dlatego tak ważne są tego typu odkrycia. Niemożliwość matematyczna, którą podobno udowodniono to Hipoteza Riemanna. Obstawiam, że mało kto wie, z czym to się je, dlatego postanowię nakreślić to najłatwiej, jak się tylko da. Zdaje sobie sprawę, że jak ludzie widzą język matematyków, to boją się tego, jak ognia. Nie jest to jednak tak straszne, jak wygląda.

Hipoteza Riemanna należy do grupy tzw. siedmiu nierozwiązanych “problemów milenijnych”.

To, co może zainteresować niektórych z Was, to nagroda, jaką można otrzymać, bo rozwiązaniu każdego z tych problemów. Instytut płaci za każdy z osobna milion dolarów. Musicie przyznać, że jest to spora sumka. Hipoteza Riemanna została sformułowana przez Bernharda Riemanna w 1859 roku. Dotyczy ona liczb pierwszych. Są to te liczby, które są większe od 1 i mają tylko dwa naturalne dzielniki — samą siebie i jedynkę. Są to niesamowicie ciekawe twory matematyczne. Według hipotezy dystrybucja liczb pierwszych nie jest przypadkowa, ale zgodna ze wzorem opisanym w specjalnej funkcji – “funkcji ζ-Riemanna“. Myk jest w tym wszystkim taki, że funkcja działa, dla znanych nam licz pierwszych, ale jak do tej pory nie mieliśmy potwierdzenia i dowodu na tę teorię. Ta jedna z jego koncepcji, to zdecydowanie jedna z największych zagadek współczesnej matematyki, która wciąż pozostaje nierozwiązana. Jeśli hipotezę udałoby kiedykolwiek się potwierdzić, być może lepiej zrozumielibyśmy, jak szukać kolejnych liczb pierwszych i jak gęsto są one rozłożone na osi liczbowej.

Ciekawe jest to, że wyżej wzmiankowany matematyk, czyli Atiyah twierdzi, że właśnie tego dokonał, stosując “drastycznie innowacyjne podejście”.

Rozwiązanie hipotezy Riemanna przedstawił podczas Heidelberg Laureate Forum w Niemczech. Tę ogromną nagrodę wyznaczył matematyczny Instytut Claya, który wymienił hipotezę Riemanna jako jeden z siedmiu największych problemów milenijnych. Prawda jest taka, że wielu próbowało już ustawić się, jako osoby, które rozwiązały ten problem, ale okazywało się, że ich rozwiązania są niepoprawne. Ostatni raz taka akcja miała miejsce w  2015 roku. Jednakże, po gruntownym sprawdzeniu przedstawianych dowodów szybko okazywało się, że hipoteza nadal będzie męczyć naukowców.

Najgorsze jest to, że aby rozwiązać ten problem sposób na przewidzenie występowania każdej liczby pierwszej.

Nie jest to takie łatwe, jakby się wydawało. To, co zaciekawiło mnie w podejściu Francisa Atiyah, to że pokazuje, iż hipoteza, mająca zdaniem niektórych stanowić klucz do rozwiązania zagadki liczb pierwszych jako fundamentu matematyki, okazała się powiązana z fizyką w o wiele większym stopniu, niż uważano dotychczas. Jako fan fizyki, jestem wręcz usatysfakcjonowany. Trzeba także zaznaczyć, że powyższy naukowiec — Sir Atiyah — oparł swój dowód na pracach takich sław, jak Von Neumann, Hirzebruch, Dirac. Ten ostatni właśnie był fizykiem. Był to jeden z twórców mechaniki kwantowej i elektrodynamiki kwantowej. Osoby związane z fizyką na pewno wiedzą, że Najważniejszym wkładem Paula A. M. Diraca w rozwój mechaniki kwantowej jest odkryte przez niego w 1928 roku równanie falowe opisujące elektron w sposób relatywistycznie niezmienniczy. Jest to istotne, ponieważ równanie to pozwoliło mu na przewidzenie istnienia pozytonu – antycząstki elektronu.

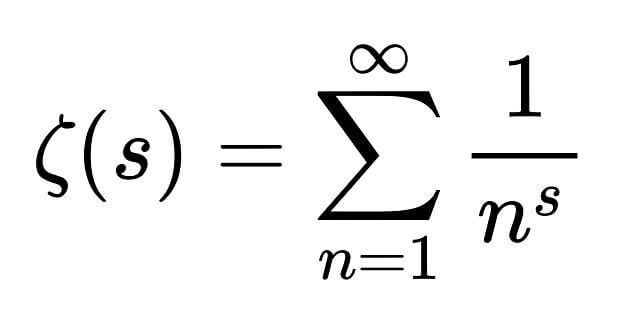
Kiedy spojrzymy na pracę Sir Michaela Francisa Atiyah, zauważymy, że celem matematyka nie było wcale udowodnienie samej hipotezy.

Jej celem było wyliczenie stałej struktury subtelnej. Jest ona oznaczona symbolem α. To podstawowa stała fizyczna określająca siłę oddziaływań elektromagnetycznych w fizyce. W tym przypadku przyjmuje się więc, że składają się na nią trzy podstawowe stałe przyrody: wartość tablicowa ładunku elektronu, prędkość światła oraz tzw. stała Plancka. Jest to zupełnie inne podejście do problemu, niż zakładano do tej pory. Ten dowód pojawił się przy okazji pracy, nad zupełnie innym problemem.

Jej problemem było to, że nikt nie był w stanie udowodnić, dlaczego ma taką wartość.

Tak właśnie zaczęła się droga do Hipotezy Riemanna. Teraz możemy się zastanowić, czy Sir Atiyahowi udało się rozwiązać  problem matematyczny dzięki połączeniu matematycznego rozumowania z tym znanym fizykom teoretycznym? Na tę chwilę większość matematyków podchodzi do nowego dowodu bardzo ostrożnie, podkreślając, że zanim zawyrokujemy o przełomie, warto poczekać na oficjalną publikację pracy, którą będzie można ocenić. Więc jeszcze nie możemy mówić o geniuszu, ale powoli możemy się do tego przygotowywać.